مطالعه خواص گاز ایده آل موضوع مهمی در فیزیک است. مقدمهای بر ویژگیهای سیستمهای گازی با در نظر گرفتن معادله بویل-ماریوت آغاز میشود، زیرا این اولین قانون آزمایشی کشفشده یک گاز ایدهآل است. بیایید آن را با جزئیات بیشتری در مقاله در نظر بگیریم.
منظور از گاز ایده آل چیست؟
قبل از صحبت در مورد قانون بویل-ماریوت و معادله ای که آن را توصیف می کند، اجازه دهید یک گاز ایده آل را تعریف کنیم. معمولاً به عنوان یک ماده سیال شناخته می شود که در آن ذرات تشکیل دهنده آن با یکدیگر برهمکنش ندارند و اندازه آنها در مقایسه با میانگین فواصل بین ذرات بسیار ناچیز است.
در واقع هر گازی واقعی است، یعنی اتم ها و مولکول های سازنده آن اندازه مشخصی دارند و به کمک نیروهای واندروالسی با یکدیگر برهمکنش ندارند. با این حال، در دماهای مطلق بالا (بیش از 300 کلوین) و فشارهای پایین (کمتر از یک اتمسفر)، انرژی جنبشی اتم ها و مولکول ها بسیار بیشتر از انرژی برهمکنش های واندروالس است، بنابراین گاز واقعی در نشان داده شده است.شرایط با دقت بالا را می توان ایده آل در نظر گرفت.
معادله بویل-ماریوت
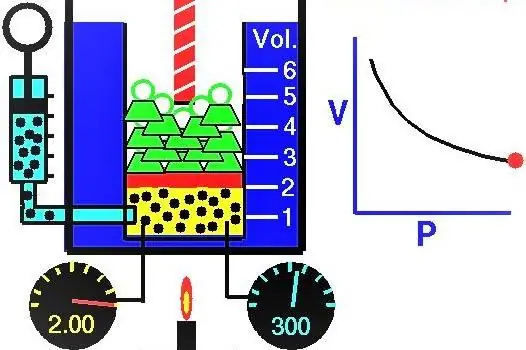
خواص گازها که دانشمندان اروپایی به طور فعال در طول قرن های هفدهم تا نوزدهم کاوش کردند. اولین قانون گازی که به صورت تجربی کشف شد، قانونی بود که فرآیندهای همدما انبساط و فشرده سازی یک سیستم گازی را توصیف می کرد. آزمایشات مربوطه توسط رابرت بویل در سال 1662 و ادم ماریوته در سال 1676 انجام شد. هر یک از این دانشمندان به طور مستقل نشان دادند که در طی یک فرآیند همدما در یک سیستم گاز بسته، فشار برعکس حجم تغییر می کند. بیان ریاضی فرآیند بهدستآمده به صورت تجربی به شکل زیر نوشته میشود:
PV=k
جایی که P و V فشار در سیستم و حجم آن هستند، k مقداری ثابت است که مقدار آن به مقدار ماده گاز و دمای آن بستگی دارد. اگر وابستگی تابع P(V) را به یک نمودار بسازید، آنگاه یک هذلولی خواهد بود. نمونه ای از این منحنی ها در زیر نشان داده شده است.
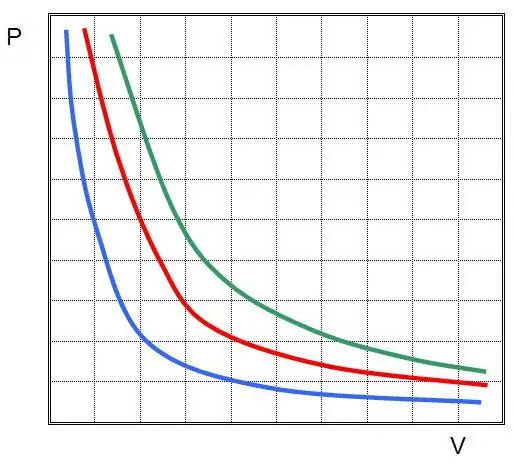
برابری نوشته شده را معادله (قانون) بویل-ماریوت می نامند. این قانون را می توان به طور خلاصه به صورت زیر فرموله کرد: انبساط یک گاز ایده آل در دمای ثابت منجر به کاهش متناسب فشار در آن می شود، برعکس، فشرده سازی همدما یک سیستم گازی با افزایش متناسب فشار در آن همراه است.
معادله گاز ایده آل
قانون بویل-ماریوت مورد خاصی از قانون کلی تر است که نام مندلیف وکلاپیرون. امیل کلاپیرون، با خلاصه کردن اطلاعات تجربی در مورد رفتار گازها در شرایط مختلف خارجی، در سال 1834 معادله زیر را به دست آورد:
PV=nRT
به عبارت دیگر، حاصل ضرب حجم V یک سیستم گازی و فشار P در آن با حاصلضرب دمای مطلق T و مقدار ماده n نسبت مستقیم دارد. ضریب این تناسب با حرف R نشان داده می شود و ثابت جهانی گاز نامیده می شود. در معادله نوشته شده، مقدار R به دلیل جایگزینی تعدادی از ثابت ها ظاهر شد که توسط دیمیتری ایوانوویچ مندلیف در سال 1874 ساخته شد.
از معادله جهانی حالت به راحتی می توان دریافت که ثبات دما و مقدار ماده تضمین کننده عدم تغییر سمت راست معادله است، به این معنی که سمت چپ معادله نیز ثابت می ماند.. در این مورد، معادله بویل-ماریوت را بدست می آوریم.

سایر قوانین گاز
معادله کلاپیرون- مندلیف که در پاراگراف بالا نوشته شده است شامل سه پارامتر ترمودینامیکی است: P، V و T. اگر هر یک از آنها ثابت باشد، و دو تای دیگر مجاز به تغییر باشند، آنگاه بویل-ماریوت را دریافت می کنیم. معادلات چارلز و گی-لوساک. قانون چارلز از تناسب مستقیم بین حجم و دما برای یک فرآیند ایزوباریک صحبت می کند و قانون گی-لوساک بیان می کند که در مورد انتقال ایزوکوریک، فشار گاز به نسبت مستقیم با دمای مطلق افزایش یا کاهش می یابد. معادلات مربوطه به این صورت است:
V/T=const وقتی P=const;
P/T=const هنگامی که V=const.
پسبنابراین قانون بویل ماریوت یکی از سه قانون اصلی گاز است. با این حال، از نظر وابستگی گرافیکی با بقیه تفاوت دارد: توابع V(T) و P(T) خطوط مستقیم هستند، تابع P(V) یک هذلولی است.
نمونه ای از یک کار برای به کارگیری قانون بویل-ماریوت
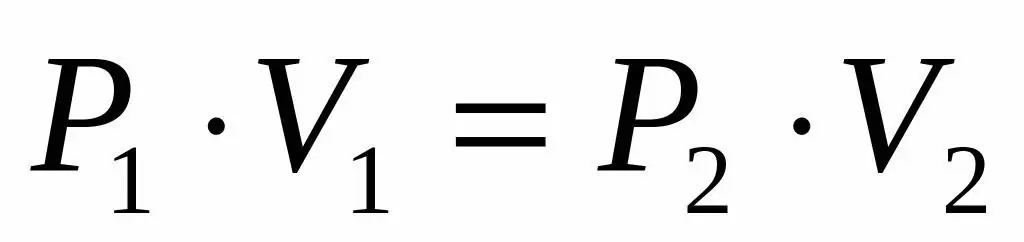
حجم گاز سیلندر زیر پیستون در موقعیت اولیه ۲ لیتر و فشار آن ۱ اتمسفر بود. فشار گاز پس از بالا آمدن پیستون و افزایش 0.5 لیتری حجم سیستم گاز چقدر بود. این فرآیند همدما در نظر گرفته می شود.
از آنجایی که فشار و حجم یک گاز ایده آل به ما داده می شود و همچنین می دانیم که دما در طول انبساط آن بدون تغییر باقی می ماند، می توانیم از معادله بویل-ماریوت به شکل زیر استفاده کنیم:
P1V1=P2V 2
این برابری می گوید که حاصلضرب فشار حجم برای هر حالت گاز در دمای معین ثابت است. با بیان مقدار P2 از برابری، فرمول نهایی را به دست می آوریم:
P2=P1V1/V 2
هنگام انجام محاسبات فشار، می توانید در این مورد از واحدهای خارج از سیستم استفاده کنید، زیرا لیترها منقبض می شوند و فشار P2 را در اتمسفر دریافت می کنیم. با جایگزینی دادههای شرط، به پاسخ سؤال میرسیم: P2=0.8 اتمسفر.






