گازها از دیدگاه ترمودینامیک با مجموعه ای از ویژگی های ماکروسکوپی توصیف می شوند که اصلی ترین آنها دما، فشار و حجم است. ثابت بودن یکی از این پارامترها و تغییر در دو پارامتر دیگر نشان می دهد که این یا آن فرآیند همسانی در گاز رخ می دهد. ما این مقاله را به پاسخ دقیق به این سؤالات اختصاص خواهیم داد که این یک فرآیند ایزوکوریک است، تفاوت آن با تغییرات همدما و ایزوباریک در حالت های یک سیستم گازی.
گاز ایده آل در فیزیک

قبل از پاسخ به این سوال که این یک فرآیند ایزوکوریک است، باید مفهوم گاز ایده آل را بهتر بشناسید. در فیزیک، به هر گازی گفته می شود که در آن میانگین انرژی جنبشی ذرات تشکیل دهنده آن بسیار بیشتر از انرژی پتانسیل برهمکنش آنها باشد و فواصل بین این ذرات چندین مرتبه بزرگتر از ابعاد خطی آنها باشد. تحت شرایط ذکر شده، در هنگام اجرا امکان پذیر استمحاسبات انرژی برهمکنش بین ذرات را در نظر نمی گیرند (برابر با صفر است) و همچنین می توان فرض کرد که ذرات نقاط مادی با جرم معین m هستند.
تنها فرآیندی که در یک گاز ایده آل انجام می شود، برخورد ذرات با دیواره ظرف حاوی ماده است. این برخوردها در عمل خود را به صورت وجود فشار معین در گاز P نشان می دهند.
به عنوان یک قاعده، هر ماده گازی که از مولکول های نسبتاً بی اثر شیمیایی تشکیل شده باشد و دارای فشار کم و دماهای بالا باشد، می تواند یک گاز ایده آل با دقت کافی برای محاسبات عملی در نظر گرفته شود.
معادله توصیف یک گاز ایده آل
البته، ما در مورد قانون جهانی کلاپیرون- مندلیف صحبت می کنیم، که باید به خوبی درک شود تا درک شود که این یک فرآیند همزون است. بنابراین، معادله جهانی حالت به شکل زیر است:
PV=nRT.
یعنی حاصل ضرب فشار P و حجم گاز V برابر است با حاصلضرب دمای مطلق T و مقدار ماده در مول n که در آن R ضریب تناسب است. خود معادله برای اولین بار توسط Emile Clapeyron در سال 1834 نوشته شد و در دهه 70 قرن 19، D. Mendeleev مجموعه ای از مقادیر ثابت یک ثابت گاز جهانی R (8.314 J/(molK) را در آن جایگزین کرد.)).
مطابق با معادله کلاپیرون- مندلیف، در یک سیستم بسته تعداد ذرات گاز ثابت می ماند، بنابراین تنها سه پارامتر ماکروسکوپی می توانند تغییر کنند (T, Pو V). واقعیت اخیر زیربنای درک فرآیندهای ایزوفرایند مختلف است که در زیر مورد بحث قرار خواهد گرفت.
فرآیند ایزوکوریک چیست؟
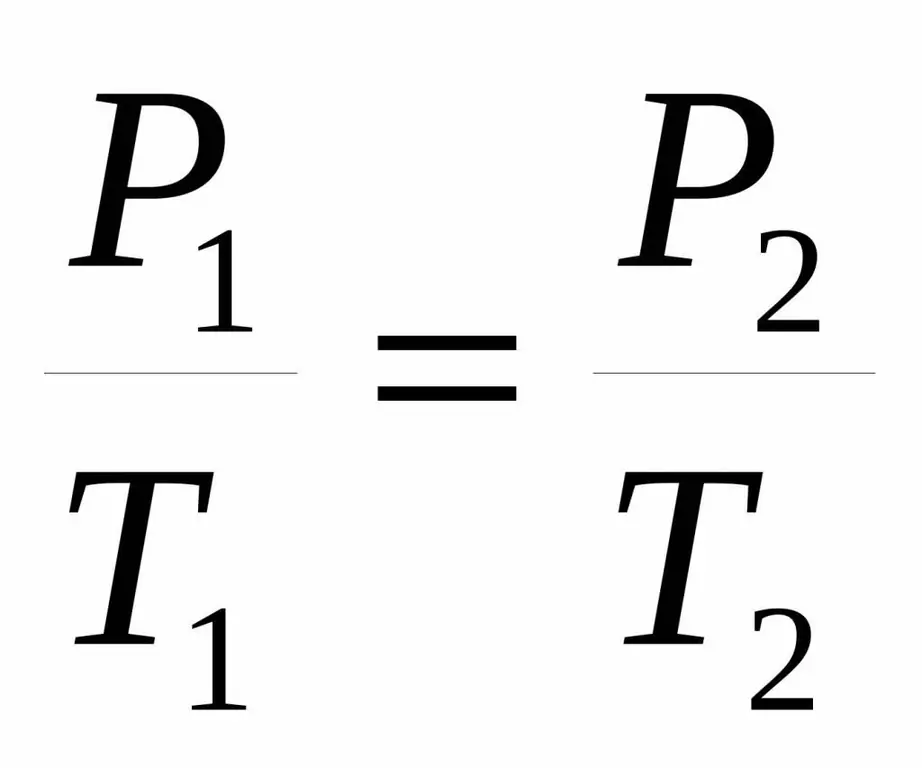
این فرآیند مطلقاً به عنوان هرگونه تغییر در وضعیت سیستم که در آن حجم آن حفظ می شود درک می شود.
اگر به معادله جهانی حالت رجوع کنیم، می توانیم بگوییم که در یک فرآیند ایزوکوریک فقط فشار و دمای مطلق در گاز تغییر می کند. برای درک دقیق چگونگی تغییر پارامترهای ترمودینامیکی، عبارت ریاضی مربوطه را می نویسیم:
P / T=Const.
گاهی اوقات این برابری به شکل کمی متفاوت ارائه می شود:
P1 / T1=P2 / T 2.
هر دو برابری را قانون شارل از نام دانشمند فرانسوی می نامند که در پایان قرن هجدهم به طور تجربی به این وابستگی اشاره کرد.

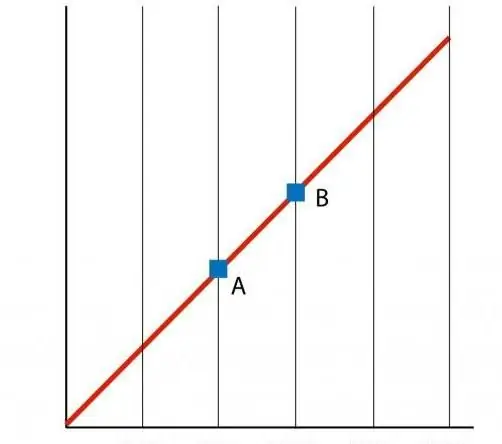
اگر نموداری از تابع P(T) بسازیم، یک وابستگی خط مستقیم به دست میآوریم که به آن ایزوکور میگویند. هر ایزوکور (برای همه مقادیر n و V) یک خط مستقیم است.
شرح انرژی فرآیند
همانطور که اشاره شد، یک فرآیند ایزوکوریک تغییری در وضعیت یک سیستم است که در یک سیستم بسته اما نه ایزوله اتفاق می افتد. ما در مورد امکان تبادل حرارت بین گاز و محیط صحبت می کنیم. به طور کلی، هر عرضه گرمای Q به سیستم منجر به دو نتیجه می شود:
- انرژی داخلی U را تغییر می دهد؛
- گازکار A، گسترش یا انقباض را انجام می دهد.
آخرین استنتاج به صورت ریاضی به صورت زیر نوشته می شود:
Q=U + A.
فرایند ایزوکوریک یک گاز ایده آل، طبق تعریفش، به معنای کار انجام شده توسط گاز نیست، زیرا حجم آن بدون تغییر باقی می ماند. این بدان معنی است که تمام گرمای ارائه شده به سیستم برای افزایش انرژی داخلی آن می رود:
Q=U.
اگر فرمول صریح انرژی داخلی را در این عبارت جایگزین کنیم، آنگاه گرمای فرآیند ایزوکوریک را می توان به صورت: نشان داد.
Q=z / 2nRT.
در اینجا z تعداد درجات آزادی است که با ماهیت چند اتمی مولکولهای سازنده گاز تعیین می شود. برای یک گاز تک اتمی z=3، برای گاز دو اتمی - 5، و برای گاز سه اتمی و بیشتر - 6. در اینجا، تحت درجات آزادی، منظور ما درجات انتقالی و چرخشی است.
اگر راندمان گرمایش یک سیستم گازی را در فرآیندهای ایزوکوریک و ایزوباریک مقایسه کنیم، در حالت اول ماکزیمم راندمان را به دست خواهیم آورد، زیرا در هنگام تغییر ایزوباریک در وضعیت سیستم، گاز منبسط می شود و بخشی از گرمای ورودی صرف انجام کار می شود.
فرایند ایزوباریک
در بالا به تفصیل توضیح دادیم که این یک فرآیند ایزوکوریک است. حال اجازه دهید چند کلمه در مورد دیگر فرآیندهای ایزو بگوییم. بیایید با ایزوباریک شروع کنیم. بر اساس نام، به عنوان انتقال سیستم بین حالت ها در فشار ثابت درک می شود. این فرآیند توسط قانون گی-لوساک به شرح زیر توصیف شده است:
V / T=Const.
همانند ایزوکور، ایزوبار V(T) نیز نشان دهنده یک خط مستقیم در نمودار است.
برایاز هر فرآیند همسان، محاسبه کار انجام شده توسط گاز راحت است، زیرا برابر است با حاصلضرب فشار ثابت و تغییر حجم.
فرایند همدما
این فرآیندی است که در آن دمای سیستم ثابت می ماند. توسط قانون بویل-ماریوت برای گاز ایده آل توصیف شده است. جالب است بدانید که این اولین قانون گاز است که به طور تجربی (نیمه دوم قرن هفدهم) کشف شد. نماد ریاضی آن به این صورت است:
PV=Const.
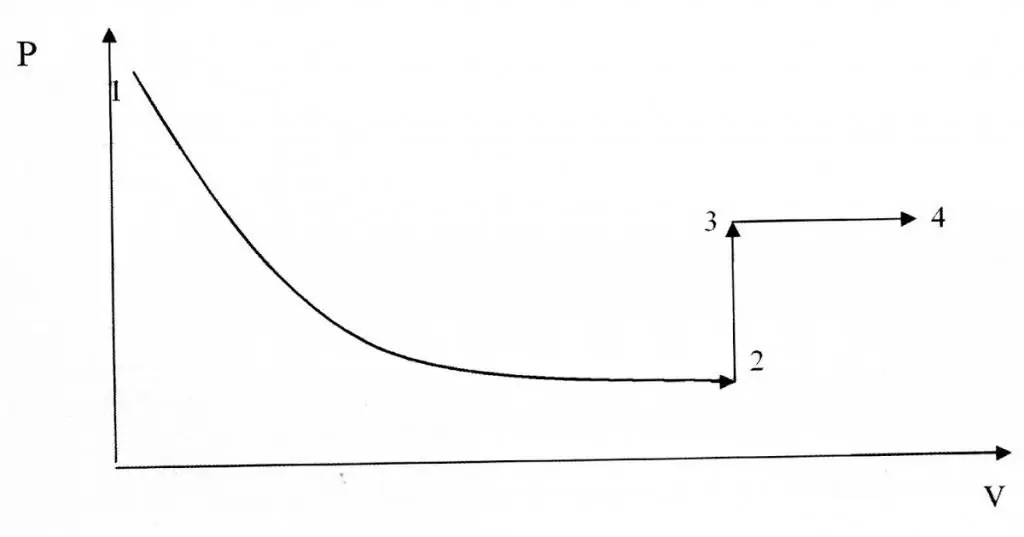
فرایندهای ایزوکوریک و همدما از نظر نمایش گرافیکی متفاوت هستند، زیرا تابع P(V) یک رابطه هذلولی است نه یک رابطه خطی.
نمونه ای از حل مسئله
بیایید اطلاعات نظری ارائه شده در مقاله را با استفاده از آنها برای حل یک مشکل عملی ادغام کنیم. مشخص است که نیتروژن گازی خالص در یک سیلندر با فشار 1 اتمسفر و دمای 25 درجه سانتیگراد قرار داشت. پس از گرم شدن سیلندر گاز و اندازه گیری فشار در آن، معلوم شد که 1.5 اتمسفر است. دمای گاز سیلندر پس از گرم شدن چقدر است؟ اگر 4 مول نیتروژن در بالون وجود داشته باشد، انرژی داخلی گاز چقدر تغییر می کند.
برای پاسخ به سوال اول از عبارت زیر استفاده می کنیم:
P1 / T1=P2 / T 2.
از کجا به دست می آوریم:
T2=P2 / P1 T 1.
در این عبارت، فشار را می توان در واحدهای دلخواه جایگزین کرداندازه گیری ها، زیرا آنها در حال کوچک شدن هستند و دما فقط بر حسب کلوین است. با این گفته، دریافت می کنیم:
T2=1.5 / 1298.15=447.224 K.
دمای محاسبه شده بر حسب درجه سانتیگراد 174 درجه سانتیگراد است.
از آنجایی که مولکول نیتروژن دو اتمی است، تغییر انرژی درونی آن در حین گرم شدن را می توان به صورت زیر تعیین کرد:
ΔU=5 / 2nRΔT.
با جایگزینی مقادیر شناخته شده در این عبارت، به پاسخ سوال دوم مسئله خواهیم رسید: ΔU=+12.4 کیلوژول.






