معادله پایه MCT و اندازه گیری دما

2024 نویسنده: Angel Austin | [email protected]. آخرین اصلاح شده: 2024-01-15 17:23

مطالعه فرآیندهای رخ داده در سیستم های آماری به دلیل حداقل اندازه ذرات و تعداد زیاد آنها پیچیده است. در نظر گرفتن هر ذره به طور جداگانه عملا غیرممکن است، بنابراین، مقادیر آماری معرفی می شوند: میانگین سرعت ذرات، غلظت آنها، جرم ذرات. فرمولی که وضعیت سیستم را با در نظر گرفتن پارامترهای میکروسکوپی مشخص می کند، معادله پایه نظریه مولکولی- جنبشی گازها (MKT) نامیده می شود.

کمی درباره سرعت متوسط ذرات

تعیین سرعت ذرات ابتدا به صورت تجربی انجام شد. یک آزمایش معروف از برنامه درسی مدرسه، که توسط اتو استرن انجام شد، ایجاد ایده ای از سرعت ذرات را ممکن کرد. در طول آزمایش، حرکت اتم‌های نقره در استوانه‌های دوار مورد مطالعه قرار گرفت: ابتدا در حالت ثابت نصب، سپس زمانی که با سرعت زاویه‌ای معینی می‌چرخید.

در نتیجه، مشخص شد که سرعت مولکول های نقره از سرعت صوت بیشتر است و 500 متر بر ثانیه است. واقعیت بسیار جالب است، زیرا برای شخص دشوار است که چنین سرعت حرکت ذرات در مواد را احساس کند.

گاز ایده آل

به تحقیق ادامه دهیدبه نظر می رسد که این فقط در سیستمی امکان پذیر است که پارامترهای آن را می توان با اندازه گیری های مستقیم با استفاده از ابزار فیزیکی تعیین کرد. سرعت با سرعت سنج اندازه گیری می شود، اما ایده وصل کردن سرعت سنج به یک ذره پوچ است. فقط یک پارامتر ماکروسکوپی مرتبط با حرکت ذرات را می توان مستقیماً اندازه گیری کرد.

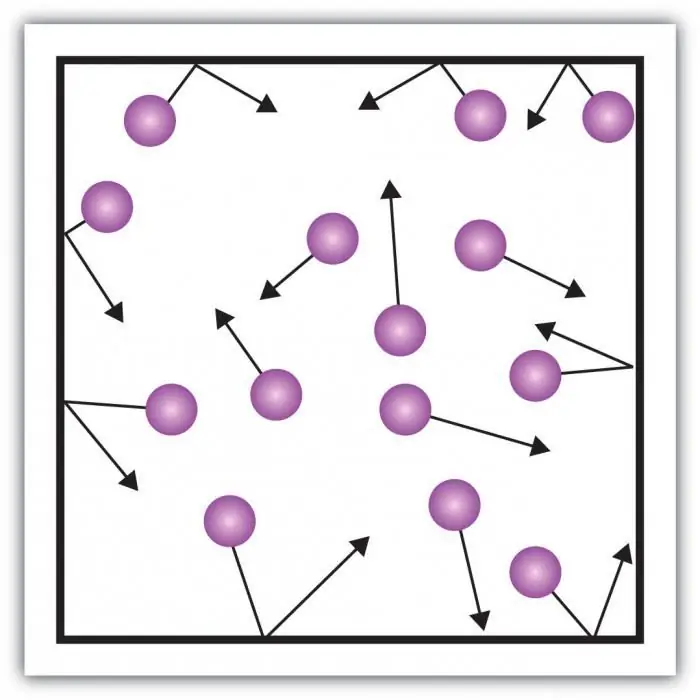
فشار گاز را در نظر بگیرید. فشار روی دیواره های ظرف در اثر برخورد مولکول های گاز در ظرف ایجاد می شود. ویژگی حالت گازی ماده در فواصل به اندازه کافی بزرگ بین ذرات و برهمکنش کوچک آنها با یکدیگر است. این به شما امکان می دهد مستقیماً فشار آن را اندازه گیری کنید.

هر سیستمی از اجسام در حال تعامل با انرژی پتانسیل و انرژی جنبشی حرکت مشخص می شود. گاز واقعی یک سیستم پیچیده است. تغییرپذیری انرژی پتانسیل خود را به سیستم سازی نمی دهد. مشکل را می توان با معرفی مدلی که دارای خواص مشخصه گاز است و پیچیدگی برهمکنش را کنار بگذارد، حل کرد.

گاز ایده آل حالتی از ماده است که در آن برهمکنش ذرات ناچیز است، انرژی پتانسیل برهمکنش به صفر می رسد. فقط انرژی حرکت که به سرعت ذرات بستگی دارد را می توان مهم در نظر گرفت.

فشار گاز ایده آل

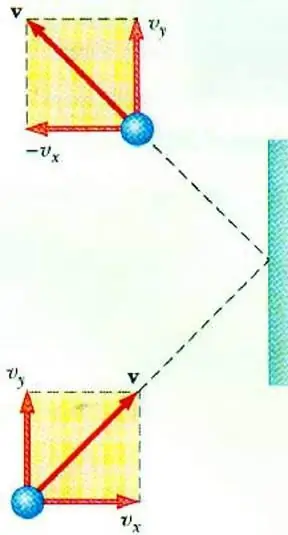
برای آشکار کردن رابطه بین فشار گاز و سرعت ذرات آن، معادله اصلی MKT یک گاز ایده آل را امکان پذیر می کند. ذره ای که در یک ظرف حرکت می کند، در اثر برخورد با دیوار، تکانه ای را به آن منتقل می کند که ارزش آن را می توان بر اساس قانون دوم تعیین کرد.نیوتن:

F∆t=2m₀v_x

تغییر تکانه یک ذره در هنگام ضربه الاستیک با تغییر مولفه افقی سرعت آن همراه است. F نیرویی است که از طرف ذره روی دیوار برای مدت کوتاهی t وارد می شود. m₀ – جرم ذره.

همه ذرات گاز در طول زمان ∆t با سطح ناحیه S برخورد می کنند و در جهت سطح با سرعت v_x حرکت می کنند و در یک استوانه با حجم Sυ قرار دارند. _{x Δt. در غلظت ذرات n، دقیقاً نیمی از مولکول ها به سمت دیواره حرکت می کنند، نیمی دیگر در جهت مخالف حرکت می کنند.}

با در نظر گرفتن برخورد همه ذرات، می توانیم قانون نیوتن را برای نیروی وارد بر منطقه بنویسیم:

F∆t=nm₀v_x^۲S∆t

از آنجایی که فشار گاز به عنوان نسبت نیروی عمود بر سطح به مساحت دومی تعریف می شود، می توانیم بنویسیم:

p=F: S=nm₀v_x^۲

رابطه حاصل به عنوان معادله اصلی MKT نمی تواند کل سیستم را توصیف کند، زیرا فقط یک جهت حرکت در نظر گرفته می شود.

توزیع ماکسول

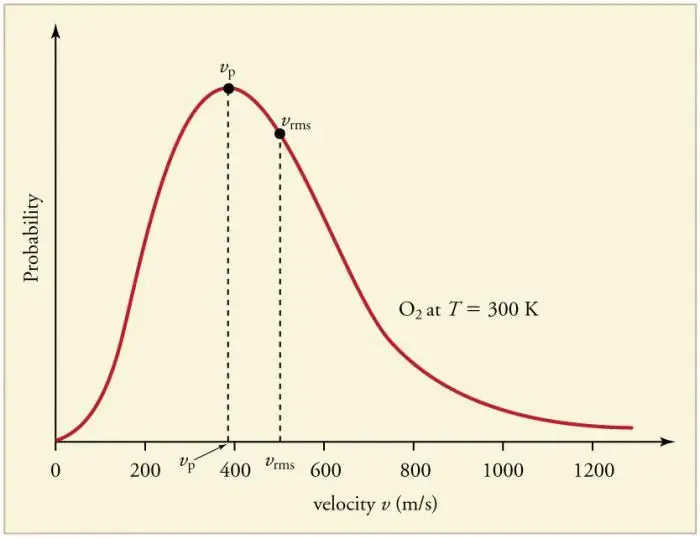
برخورد مکرر ذرات گاز با دیواره ها و با یکدیگر منجر به ایجاد توزیع آماری معینی از ذرات از نظر سرعت (انرژی) می شود. جهت همه بردارهای سرعت به یک اندازه محتمل است. این توزیع را توزیع ماکسول می نامند. در سال 1860 این الگو بودمشتق شده توسط J. Maxwell بر اساس MKT. پارامترهای اصلی قانون توزیع سرعت نامیده می شوند: محتمل، مربوط به حداکثر مقدار منحنی، و ریشه میانگین مربع v_kv=√‹v² › - مجذور میانگین سرعت ذرات.

افزایش دمای گاز با افزایش سرعت مطابقت دارد.

بر اساس این واقعیت که همه سرعت ها برابر هستند و ماژول های آنها مقدار یکسانی دارند، می توانیم فرض کنیم:

‹v²›=‹v_x²› + ‹v y2^{› + ‹v}z2^{›، از: ‹ v}x2^›=‹v2^{›: 3}

معادله اصلی MKT، با در نظر گرفتن مقدار متوسط فشار گاز، این است:

p=nm₀‹v²›: 3.

این رابطه از این نظر منحصر به فرد است که رابطه بین پارامترهای میکروسکوپی را تعیین می کند: سرعت، جرم ذرات، غلظت ذرات و فشار گاز به طور کلی.

با استفاده از مفهوم انرژی جنبشی ذرات، معادله اصلی MKT را می توان متفاوت بازنویسی کرد:

p=2nm₀‹v²›: 6=2n‹E_k›: 3

فشار گاز متناسب با مقدار متوسط انرژی جنبشی ذرات آن است.

دما

جالب توجه است که برای مقدار ثابتی از گاز در یک ظرف بسته، می توان فشار گاز و مقدار متوسط انرژی حرکت ذرات را به هم مرتبط کرد. در این حالت فشار را می توان با اندازه گیری انرژی اندازه گیری کردذرات.

چه باید کرد؟ چه مقداری را می توان با انرژی جنبشی مقایسه کرد؟ به نظر می رسد دما چنین مقداری است.

دما معیاری برای سنجش حالت حرارتی مواد است. برای اندازه گیری آن از یک دماسنج استفاده می شود که اساس آن انبساط حرارتی سیال کار (الکل، جیوه) هنگام گرم شدن است. مقیاس دماسنج به صورت تجربی ایجاد شده است. معمولاً علائم مربوط به موقعیت سیال کار در طول برخی از فرآیندهای فیزیکی که در یک حالت حرارتی ثابت (آب جوش، ذوب یخ) اتفاق می افتد، روی آن قرار می گیرند. دماسنج های مختلف مقیاس های متفاوتی دارند. به عنوان مثال، درجه سانتیگراد، فارنهایت.

مقیاس دمای جهانی

دماسنج های گازی را می توان از نظر استقلال از خواص سیال عامل جالب تر در نظر گرفت. مقیاس آنها به نوع گاز مورد استفاده بستگی ندارد. در چنین دستگاهی، به طور فرضی می توان دمایی را که در آن فشار گاز به صفر میل می کند، مشخص کرد. محاسبات نشان می دهد که این مقدار با -273.15 ^oC مطابقت دارد. مقیاس دما (مقیاس دمای مطلق یا مقیاس کلوین) در سال 1848 معرفی شد. دمای احتمالی فشار گاز صفر به عنوان نقطه اصلی این مقیاس در نظر گرفته شد. یک بخش از مقیاس برابر با مقدار واحد مقیاس سانتیگراد است. به نظر می رسد نوشتن معادله اصلی MKT با استفاده از دما هنگام مطالعه فرآیندهای گاز راحت تر است.